O canal Veritasium publicou um vídeo muito interessante contanto to o percurso percorrido nos últimos 100 anos até chegarmos no modelo de Black-Scholes-Merton. Ele também mostra como esse modelo impactou o mercado financeiro.

O vídeo ficou muito interessante e conta com a participação do Andrew Lo para explicar detalhes mais técnicos.

Como as legendas são estão disponíveis em inglês, traduzi a transcrição e disponibilizo aqui.

Transcrição:

A equação de Black-Scholes-Merton

Essa equação única gerou quatro indústrias de vários trilhões de dólares e transformou a de todos abordagem do risco.

“Você acha que a maioria das pessoas está ciente do tamanho, escala, utilidade dos derivativos?”

“Não, não faz ideia.”

Mas em seu cerne essa equação vem da física, da descoberta de átomos, entender como o calor é transferido e como vencer o cassino no blackjack.

Então, talvez não deva ser surpreendente que alguns dos melhores para bater o mercado de ações não eram traders veteranos, mas físicos, cientistas e matemáticos.

Em 1988, um professor de matemática chamado Jim Simons criou o Medallion Investment Fund e todos os anos, pelos próximos 30 anos, o Fundo Medallion entregou retornos superiores à média do mercado.

E não só por pouco, rendeu 66% ao ano. A esse ritmo de crescimento, 100 dólares investidos em 1988 valeriam 8,4 bilhões de dólares hoje.

Isso fez de Jim Simons facilmente o matemático mais rico de todos os tempos.

Mas ser bom em matemática não garante sucesso nos mercados financeiros. Basta perguntar a Isaac Newton.

Em 1720, Newton tinha 77 anos e era rico. Ele tinha ganhado muito dinheiro trabalhando como professor em Cambridge por décadas e ele teve um lado como o mestre da casa da moeda real.

Seu patrimônio líquido era de 30.000 libras, o equivalente a 6 milhões de dólares hoje.

Agora, para aumentar sua fortuna, Newton investiu em ações. Uma de suas grandes apostas foi na South Sea Company.

Seu negócio era transportar africanos escravizados através do Atlântico.

Os negócios estavam crescendo e o preço das ações cresceu rapidamente. Em abril de 1720, o valor das ações dobrou, então ele vendeu suas ações. Mas o preço das ações continuou subindo e em junho

Newton recomprou e continuou comprando ações mesmo com o pico do preço.

Quando o preço começou a cair, Newton não vendeu. Ele comprou mais ações achando que estava comprando o mergulho. Mas não houve recuperação e, finalmente, ele perdeu cerca de um terço de sua riqueza. Quando perguntado por que ele não viu isso vindo, Newton respondeu: eu posso calcular os movimentos dos corpos celestes, mas não a loucura das pessoas.

Então, o que Simons acertou que Newton errou?

Bem, por um lado, Simons foi capaz de ficar sobre os ombros de gigantes.

A matemática dos passeios aleatórios

como Louis Bachelier, Albert Einstein e outros matemáticos e físicos descobriram e aplicaram a teoria dos passeios aleatórios para modelar fenômenos como o movimento browniano, a difusão do calor e os preços das ações.

O pioneiro do uso da matemática para modelar os mercados financeiros foi Louis Bachelier, nascido em 1870. Seus pais morram quando ele tinha 18 anos e ele teve que assumir o negócio de vinho de seu pai.

Ele vendeu o negócio alguns anos depois e se mudou para Paris para estudar física. Mas ele precisava de um emprego para se sustentar.

Ele e sua família encontraram um na Bourse, a bolsa de valores de Paris.

E lá dentro estava a loucura de Newton com as pessoas em sua forma mais rara. Centenas de traders gritando preços, fazendo sinais de mão e fazendo negócios. Mas o que despertou o interesse de Bachelier foram os contratos conhecidas como opções.

As primeiras opções conhecidas foram compradas por volta de 600 a.C. pelo filósofo grego Tales de Mileto. Ele acreditava que o próximo verão renderia uma safra de azeitonas.

Para ganhar dinheiro com essa ideia, ele poderia ter comprado prensas de azeitonas que, se ele estivesse certo seria muito procurado. Mas ele não tinha dinheiro suficiente para comprar as máquinas, então ele foi a todos os proprietários de lagares de azeitonas existentes e pagou-lhes um pouco de dinheiro para garantir a opção de alugar suas prensas no verão por um preço especificado. Quando a colheita chegou, Thales estava certo.

 Havia tantas azeitonas que o preço de alugar uma prensa disparou. Thales pagou o preço pré-acordado e depois alugou as máquinas a uma taxa mais alta e embolsou a diferença.

Thales executou a primeira opção de compra conhecida. Uma opção de compra (call) dá-lhe o direito, mas não a obrigação de comprar algo em uma data posterior por um preço definido conhecido como strike.

Você também pode comprar uma opção de venda que lhe dá o direito, mas não a obrigação de vender algo em uma data posterior para o preço de exercício. Opções de venda são úteis se você espera que o preço caía. As opções de compra são úteis se você espera que o preço suba.

Por exemplo, digamos que o atual preço das ações da Apple é de 100 dólares, mas você espera que ele suba. Você pode comprar uma opção de compra por 10 dólares que lhe dá o direito, mas não a obrigação de comprar ações da maçã em até um ano por 100 dólares.

Esse é o preço de exercício.

Apenas uma pequena nota: as opções americanas podem ser exercidas em qualquer data até ao termo do prazo, ao passo que as opções europeias devem ser exercidas no termo do prazo.

Para manter as coisas simples, vamos nos ater às opções europeias. Então, se em um ano o preço das ações da Apple subiu para 130 você pode usar a opção de comprar ações por 100 dólares e, em seguida, imediatamente vendê-los por 130.

Depois de levar em conta os dez dólares que você pagou pela opção, você fez um lucro de 20 dólares. Alternativamente, se em um ano os preços das ações caíram para setenta dólares você simplesmente não usaria a opção e você perdeu os 10 dólares que pagou por ela.

Assim, o lucro e o diagrama de perda têm esta aparência.

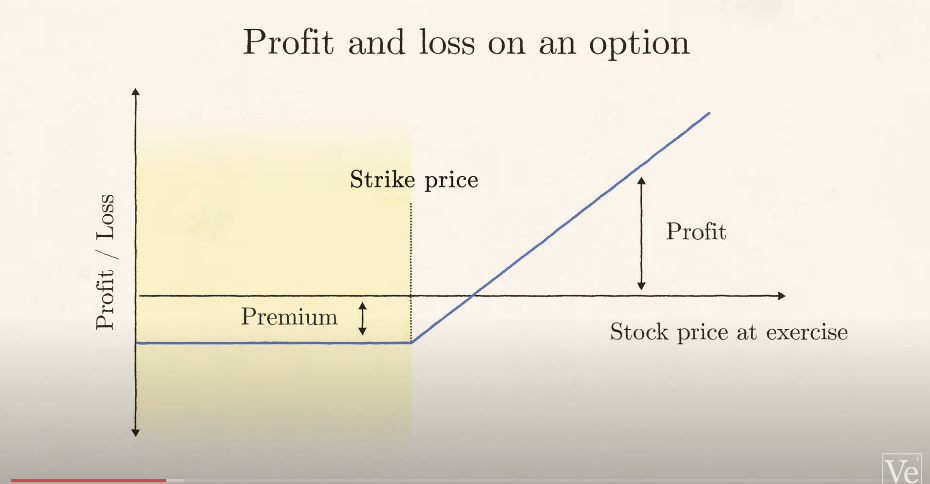
Se o preço da ação acabar abaixo do preço de exercício, você perde o que você pagou pela opção, mas se o preço da ação for maior do que o preço de exercício, então você ganha a diferença menos o custo da opção.

Há pelo menos três vantagens das opções.

Uma delas é que limita o seu lado negativo. Se você tivesse comprado a ação em vez da opção e ela caiu a setenta dólares você teria perdido trinta dólares e em teoria você poderia ter perdido 100 dólares se o estoque fosse a zero.

O segundo benefício são as opções que proporcionam alavancagem.

Se você tivesse comprou a ação e subiu para cento e trinta dólares, então seu investimento cresceu em 30%. Mas se você tivesse comprado a opção, você só tinha que colocar até dez dólares para o seu lucro de vinte dólares é, na verdade, um retorno de duzentos por cento sobre o investimento.

No lado negativo, se você tivesse a ação, seu investimento teria caído apenas trinta por cento enquanto com a opção você perde todos 100%.

Então, com a negociação de opções, há uma chance para obter lucros muito maiores, mas também perdas muito maiores.

O terceiro benefício é que você pode usar opções como um hedge. Acho que a motivação original para as opções foi descobrir uma maneira de reduzir o risco e depois, é claro, uma vez que as pessoas decidiram que queriam comprar um seguro, isso significava que há outras pessoas lá fora que queriam vendê-lo com lucro e é assim que os mercados são criados.

Portanto, as opções podem ser uma ferramenta de investimento incrivelmente útil, mas o que Bachelier viu no pregão foi o caos, especialmente quando se tratava do preço das opções de ações. Mesmo que eles estivessem por aí, por centenas de anos ninguém havia encontrado uma boa maneira de precificá-los.

Os traders apenas negociariam para vir a um acordo sobre qual deve ser o preço. Dada a opção de comprar ou vender algo no futuro parece um tipo muito amorfo de um comércio e, portanto, chegando a preços para estes objetos bastante estranhos tem sido um desafio que tem atormentado vários economistas e empresários há séculos.

Agora Bachelier já interessado em probabilidade achava que tinha que haver uma solução matemática para este problema e ele propôs este como seu tema de doutorado para seu orientador Henri Poincaré.

Olhar para a matemática das finanças não era realmente algo que as pessoas faziam naquela época, mas, para surpresa de Bachelier, Poincaré concordou.

Para precificar com precisão uma opção primeiro você precisa saber o que acontece com os preços das ações ao longo do tempo. O preço de uma ação é basicamente definido por um cabo de guerra entre compradores e vendedores.

Quando mais pessoas querem comprar uma ação, o preço sobe. Quando mais pessoas quer vender uma ação o preço cai. Mas o número de compradores e vendedores pode ser influenciado por quase qualquer coisa como o clima, política, novos concorrentes, inovação e assim por diante.

Então Bachelier percebeu que é praticamente impossível prever todos esses fatores com precisão. Assim, o melhor que você pode é assumir que, a qualquer momento, o preço das ações tem a mesma probabilidade de subir quanto de descer e portanto, no longo prazo, os preços das ações seguem um passeio aleatório se movendo para cima e para baixo como se o próximo movimento fosse determinado pelo lançamento de uma moeda.

A aleatoriedade é uma marca de um mercado eficiente.

Por economistas eficientes normalmente significa que você não pode ganhar dinheiro negociando. A ideia de que você não deve ser capaz de comprar um ativo e vendê-lo imediatamente para obter lucro é conhecido como Hipótese dos Mercados Eficientes.

Quanto mais as pessoas tentam ganhar dinheiro prevendo o mercado de ações e então negociam com essas previsões, menos previsíveis são esses preços. Se você e eu pudéssemos prever o mercado de ações amanhã então nós faríamos isso. Começaríamos a negociar hoje em ações que achava que ia subir amanhã. Bem, se fizéssemos isso, em vez de subir amanhã eles subiam agora à medida que comprávamos cada vez mais ações.

Portanto, o próprio ato de prever na verdade, afeta a qualidade dos resultados futuros. E assim em um mercado totalmente eficiente os preços de amanhã não podem ter qualquer poder preditivo. Se o fizessem, teríamos aproveitou hoje.

Este é um tabuleiro de Galton. Tem fileiras de estacas dispostas em um triângulo e cerca de 6000 rolamentos de esferas minúsculos que posso derramar através das estacas. Agora, cada vez que uma bola bate uma estaca há uma chance de 50-50 de ir para a esquerda ou para a direita. Assim, cada bola segue um passeio aleatório como ele passa por essas estacas, o que torna basicamente impossível prever o caminho de qualquer bola individual.

Mas se eu virar isso o que você pode ver é que todas as bolas juntas sempre

Crie um padrão previsível. Ou seja, uma coleção de passeios aleatórios cria uma distribuição normal.

É centrado no meio porque o número de caminhos que uma bola pode tomar para chegar até aqui é o E quanto mais longe você for, menos caminhos uma bola poderia tomar para chegar lá. Como se você quer acabar aqui bem a bola teria que ir para a esquerda todo o caminho para baixo para que haja só uma maneira de chegar aqui, mas para chegar ao meio há milhares de caminhos que uma bola poderia tomar.

Agora, Bachelier acreditava que o preço de uma ação é como uma bola passando por um tabuleiro de Galton.

Cada camada adicional de estacas representa um passo de tempo para que, após um curto período de tempo, o preço das ações possa apenas subir ou descer um pouco, mas depois de mais tempo uma gama mais ampla de preços é possível.

De acordo com Bachelier o preço futuro esperado de uma ação é descrito por uma distribuição normal centrada no preço atual que se espalha ao longo do tempo. Bachelier percebeu que havia redescoberto o exato equação que descreve como o calor irradia de regiões de alta temperatura para regiões de baixa temperatura.

Isso foi descoberto pela primeira vez por Joseph Fourier em 1822, então Bachelier chamou de seu descobrir a radiação de probabilidades. Desde que ele estava escrevendo sobre finanças a comunidade de física não tomou conhecimento, mas a matemática do passeio aleatório passaria a resolver um quase mistério centenário na física.

Em 1827, o botânico escocês Robert Brown estava olhando para grãos de pólen sob o microscópio e ele notou que as partículas suspensas em água no microscópio. Os slides estavam se movendo aleatoriamente. Porque ele não sabia se era algo a ver com sendo o pólen material vivo ele testou partículas não orgânicas, como poeira de lava e rocha de meteorito.

Novamente ele os viu se movendo da mesma maneira, então Brown descobriu que quaisquer partículas, se fossem pequenas o suficiente, exibiam esse movimento aleatório que veio a ser conhecido como Movimento browniano. Mas o que causou isso permaneceu um mistério. 80 anos depois, em 1905, Einstein descobriu: saiu a resposta.

Nos duzentos anos anteriores, a ideia de que gases e líquidos foram feitos de moléculas tornaram-se cada vez mais populares, mas nem todos estavam convencidos de que as moléculas eram real em um sentido físico só que a teoria explicou um monte de observações. A ideia levou Einstein levantar a hipótese de que o movimento browniano é causado pelos trilhões de moléculas que atingem as partículas de todas as direções a cada instante.

Ocasionalmente vai bater mais de um lado do que do outro e as partículas saltarão momentaneamente. Para derivar a matemática, Einstein supôs que como observador, não podemos ver ou prever essas colisões com certeza, então em nenhum momento temos que assumir que a partícula tem a mesma probabilidade de se mover em uma direção como em outra.  

Então assim como os preços das ações, partículas microscópicas se movem como uma bola caindo em uma placa de Galton.

A localização esperada de uma partícula é descrita por uma distribuição normal que se amplia com o tempo.

É por isso que mesmo em água completamente parada, partículas microscópicas se espalham. Isso é difusão. Ao resolver o mistério do movimento browniano, Einstein havia encontrado evidências definitivas de que os átomos e moléculas existem. Claro que ele não tinha ideia de que Bachelier havia descoberto o passeio aleatório cinco anos antes.

 Quando Bachelier terminou seu doutorado, ele finalmente descobriu uma maneira matemática de precificar uma opção. Lembre-se que com uma opção de compra se o preço futuro de uma ação for menor que o preço de exercício, então você perde o prêmio pago pela opção, mas se o preço da ação for maior do que o preço de exercício você embolsa essa diferença e você faz um lucro líquido se a ação tiver ido acima de mais do que você pagou pela opção.

Portanto, a probabilidade de que um comprador de opções obtenha lucro é a probabilidade de que o preço aumente mais do que o preço pago por ele, que é a área sombreada verde e a probabilidade de que o vendedor ganhe dinheiro é apenas a probabilidade de que

O preço permanece baixo o suficiente para que o comprador não ganhe mais do que pagou por ele. Este é a área sombreada de vermelho.

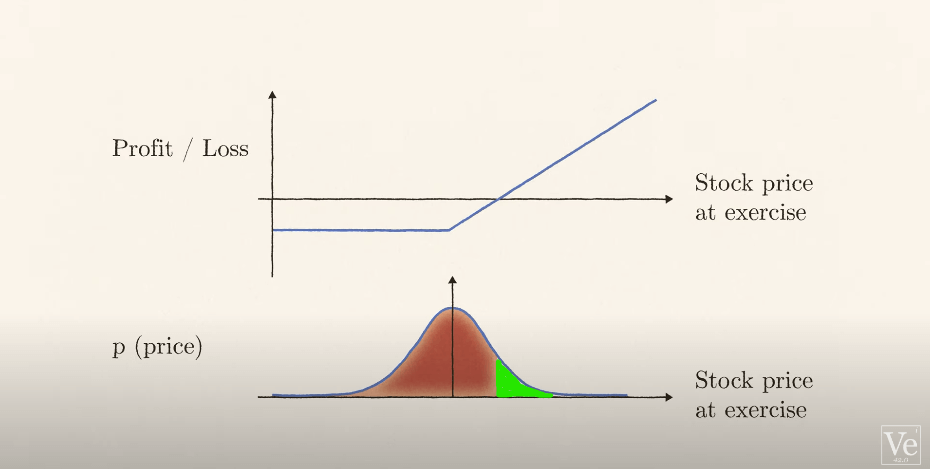
Multiplicando o lucro ou perda pela probabilidade de cada resultado calculado por Bachelier o retorno esperado de uma opção. Agora, quanto deve custar? Se o preço de uma opção for demais alto ninguém vai querer comprá-lo. Por outro lado, se o preço for muito baixo, todos vão querer comprá-lo.

Bachelier argumentou que o preço justo é o que torna o retorno esperado para compradores e vendedores igual.

Ambas as partes devem ganhar ou perder o mesmo montante.

Essa foi a visão de Bachelier sobre como precificar com precisão uma opção. Quando Bachelier terminou o seu doutorado ele havia vencido Einstein para inventar o passeio aleatório e resolvido o problema que tinha escapado aos traders de opções por centenas de anos, mas ninguém notou.

Os físicos foram desinteressados e os traders não estavam prontos. O que faltava era uma maneira de ganhar muito dinheiro.

A arte de vencer o mercado

como Ed Thorp, Jim Simons e outros gênios da matemática usaram a contagem de cartas, o hedge dinâmico, o machine learning e outras estratégias baseadas em dados para encontrar padrões e ineficiências no mercado de ações e obter retornos extraordinários.

Na década de 1950 um jovem formado em física, Ed Thorp, estava fazendo seu PhD em Los Angeles, mas a poucas horas de carro de Las Vegas estava rapidamente se tornando a capital mundial do jogo e Thorp viu uma maneira de fazer uma fortuna.

Dirigiu-se a Vegas e sentou-se à mesa de blackjack. Naquela época, o dealer só usava um único baralho de cartas para que Thorp pudesse manter uma nota mental de todas as cartas que haviam sido jogadas como ele os viu.

Isso permitiu que ele descobrisse se tinha uma vantagem. Ele apostaria uma parcela maior de seus fundos quando as probabilidades estavam a seu favor e menos quando não estavam. Ele tinha inventado a contagem de cartas. Esta é uma inovação notável, considerando que o blackjack já existia há centenas de anos e por um tempo isso lhe rendeu muito dinheiro, mas os cassinos descobriram a sua estratégia e eles adicionaram mais baralhos de cartas ao jogo para reduzir o benefício da contagem de cartas, então Thorp levou seus ganhos para o que ele chamou de o maior cassino do mundo, o mercado de ações.

Ele começou um fundo de hedge que passaria a ter um retorno de 20% a cada ano por 20 anos, o melhor desempenho já visto naquela época e ele fez isso transferindo as habilidades que aprimorou no blackjack para o mercado de ações.

Thorp foi pioneiro em um tipo de hedge, uma forma de proteção contra perdas com operações de balanceamento ou compensação. Thorp fez isso matematicamente, ele olhou para as chances de ganhar e perdendo e decidiu que, sob certas condições, você pode realmente inclinar as probabilidades ao seu favor usando certos padrões para poder fazer apostas.

Suponha que Bob venda a Alice uma opção de compra em uma ação e digamos que a ação subiu, então agora está no dinheiro para Alice. Bem, agora para a cada dólar a mais o preço das ações sobe, Bob perderá um dólar, mas ele pode eliminar esse risco por possuir uma unidade de ação, então, se o preço subir, ele perderia um dólar com a opção, mas ganharia esse dólar de volta da ação e se a ação cair de volta ao dinheiro para Alice vende as ações para não correr o risco de perder dinheiro com isso. Isso é chamado de hedge dinâmico e significa que Bob pode obter lucro com risco mínimo de flutuação dos preços das ações.

Uma carteira coberta pi a qualquer momento compensará a opção v com alguma quantidade delta de ações.

Basicamente, significa que posso vender-lhe algo sem ter que tomar o lado oposto de a maneira de pensar sobre isso é que eu fabriquei sinteticamente uma opção para você.

Eu criei-o do nada, fazendo hedge dinâmico de negociação.

Como vimos com o exemplo de Bob, delta é a quantidade de ações que ele tem que manter muda dependendo dos preços atuais.

Matematicamente, ele representa o quanto o preço atual da opção muda com uma mudança no preço da ação, mas Thorp não estava satisfeito com o modelo da Bachelier para precificação de opções. Quero dizer, por um lado, os preços das ações não são totalmente aleatórios, eles podem aumentar com o tempo se o negócio estiver indo bem ou cair se não for.

O modelo de Bachelier ignorou isso, então Thorp criou um modelo mais preciso para preços de opções que levassem em conta essa derivada.

“Eu realmente descobri o que esse modelo em meados de 1967 e eu decidi que eu iria usá-lo apenas para mim e depois eu mantive isso em silêncio para meus próprios investidores. A ideia era basicamente ganhar muito dinheiro com isso para todos.”

Sua estratégia era se a opção estava saindo barata de acordo com seu modelo comprá-la se estava supervalorizado vender a descoberto que é aposta contra ele e assim na maioria das vezes ele acabaria até o lado vencedor da troca.

Isso durou até 1973. Naquele ano Fisher Black e Myron Scholes criou uma equação que mudou a indústria. Robert Merton publicado de forma independente sua própria versão que foi baseada na matemática do cálculo estocástico, então ele também é creditado.

“Eu pensei que eu teria o campo para mim, mas infelizmente Fisher Black e Myron Scholes publicaram a ideia e eles fizeram um trabalho melhor do modelo do que eu porque eles tinham uma matemática muito apurada por trás de sua derivação”

Como Bachelier, eles achavam que os preços das opções deveriam oferecer uma aposta justa para compradores e vendedores, mas sua abordagem era totalmente nova.

Eles disseram que se era possível construir uma carteira livre de risco de opções e ações assim como Thorp estava fazendo com seu hedge delta então em um mercado eficiente um mercado justo a carteira não deve devolver nada mais do que a taxa livre de risco que o mesmo dinheiro ganharia se investido no ativo mais seguro dos títulos do Tesouro dos EUA.

A suposição era que, se você não está assumindo qualquer risco adicional, então não deve ser possível receber nenhum retorno extra.

Para descrever como os preços das ações mudam ao longo do tempo, Black Scholes e Merton usaram uma versão melhorada:

do modelo de Bachelier, assim como Thorp. Isso diz que, a qualquer momento, esperamos que o preço das ações se mova aleatoriamente mais uma tendência geral para cima ou para baixo. Combinando essas duas equações Black, Scholes e Merton criaram a equação mais famosa das finanças.

Ela relaciona o preço de qualquer tipo de contrato para qualquer ativo ações títulos que você nomeia. No mesmo ano em que eles publicaram esta equação foi fundada a bolsa de opções de Chicago. Por que essa equação é tão importante para as finanças?

Como isso mudou o jogo? Bem, porque quando você resolve essa equação diferencial parcial você obtém uma fórmula explícita do preço da opção em função de um monte desses parâmetros e pela primeira vez agora você tem uma expressão explícita onde você se conecta os parâmetros e para fora aparece este número para que as pessoas possam realmente usá-lo para negociar.

Isso levou a uma das mais rápidas adoções pela indústria de uma ideia acadêmica em todas as ciências sociais.

Em apenas alguns anos, a fórmula Black Scholes foi adotada como referência para Wall Street para negociação de opções. O mercado de opções negociadas em bolsa explodiu e agora é uma indústria multitrilionária. O volume nesse mercado vem dobrando a cada cinco anos portanto, este é o equivalente financeiro da lei de Moore.

Há outros negócios que cresceram tão rapidamente quanto os swaps de inadimplência de crédito comercializam o mercado de derivativos OTC a dívida securitizada.

Todas essas são indústrias de trilhões de dólares que, de uma forma ou de outra, fazem uso da ideia de precificação de opções Black-Scholes-Merton.

Isso abriu uma nova maneira de se proteger contra qualquer coisa e não apenas para fundos de hedge. Hoje em dia praticamente todas as grandes empresas governos e mesmo os investidores individuais usam opções para se proteger contra seus próprios riscos específicos.

Suponha que você esteja administrando uma companhia aérea e esteja preocupado que um aumento nos preços do petróleo coma seus lucros. Bem, usando a equação de Black-Scholes-Merton, há uma maneira de se proteger eficientemente esse risco. Você precifica uma opção para comprar algo que rastreia o preço do petróleo e essa opção compensará se os preços do petróleo subirem e isso ajudará a compensá-lo pela alta no custo do combustível você tem que pagar.

Assim, Black Scholes Merton pode ajudar a reduzir o risco, mas também pode fornecer alavancagem.

Uma batalha contínua entre day traders de alta e vendedores a descoberto de fundos de hedge que apostaram contra as ações da GameStop já subiram cerca de 700%.

“Bem GameStop é um exemplo realmente interessante por todos os tipos de razões, mas as opções figuraram com destaque nisso exemplo porque um pequeno grupo de usuários neste subcanal do Reddit WallStreetBets decidiu que os gestores de fundos de hedge que estavam vendendo as ações e apostando que a empresa sairia de negócios precisava ser punido e por isso compraram ações da GameStop para tentar dirigir preço acima.

Acontece que comprar a ação não era suficiente, porque com um dólar em dinheiro você pode comprar ações no valor de um dólar, mas com o valor de um dólar em dinheiro você pode comprar opções.

Isso afetou muito mais do que o valor de um dólar em ações, talvez em alguns casos 10 ou 20 dólares; valor de ações por um dólar de opções e, portanto, há alavancagem natural embutida nelas e, portanto, a combinação de comprar tanto a ação quanto as opções fez com que os preços O que isso fez foi fazer com que esses gestores de fundos de hedge perdessem muito dinheiro rápido.”

Qual o tamanho desse mercado de derivativos? Quão grande é toda essa área que meio que sai de Black-Scholes-Merton?

“Há estimativas de quão grandes são os mercados de derivativos e primeiro deixar claro o que é um derivado. Um derivativo é um título financeiro cujo valor deriva de outro ativo financeiro. Portanto, uma opção é um exemplo de um derivado.

Em geral, o tamanho dos mercados de derivativos globalmente é da ordem de várias centenas trilhões de dólares.”

Como isso se compara ao tamanho dos títulos subjacentes em que se baseiam?

“São múltiplos dos títulos subjacentes.”

Eu só tenho que interromper porque parece gentil de louco que você tem mais dinheiro cavalgando nas coisas que são baseadas na coisa do que a coisa em si.

“Está correto.”

Então me diga como isso faz algum sentido?

“Porque o que as opções permitem que você faça é pegar a coisa subjacente e transformá-la em 5, 10, 20, 50 coisas. Então esses pedaços de papel que chamamos de opções e derivativos eles basicamente nos permitem criar muitas versões diferentes do ativo subjacente. Versões que os indivíduos encontram mais palatável por causa de suas próprias preferências de recompensa de risco.”

Isso faz com que os mercados e a economia global mais estável ou menos estável ou sem efeito?

Os três. Acontece que em tempos normais, estes mercados são uma fonte muito significativa de liquidez e, por conseguinte, estabilidade. Em tempos anormais, refiro-me a períodos de estresse do mercado todos esses títulos podem ir em uma direção tipicamente para baixo e quando eles caem juntos. Isso cria uma quebra de mercado muito grande.

Assim, nessas circunstâncias, os mercados de derivados podem: exacerbar esses tipos de deslocamentos de mercado.”

Em 1997, Merton e Scholes foram premiados com o Prêmio Nobel de Economia. Black foi reconhecido por suas contribuições, mas infelizmente ele teve faleceu apenas dois anos antes.

“Vamos ganhar muito dinheiro em opções, mas agora Black e Scholes contaram a todos qual é o segredo. Com a fórmula de preços de opções agora para que todos possam ver os fundos de hedge precisariam descobrir melhores maneiras de encontrar ineficiências de mercado”.

Entra Jim Simons. Antes de Simons ter qualquer exposição ao mercado de ações, ele era matemático.

Seu trabalho sobre geometria de Riemann foi fundamental em muitas áreas da matemática e física, incluindo: teoria dos nós, teoria quântica de campos e computação quântica, a teoria de Chern.

Simons estabeleceu os fundamentos matemáticos para a teoria das cordas. Em 1976 a Sociedade Americana de Matemática apresentou ele com o Prêmio Oswald Veblen em geometria, mas no topo de sua carreira acadêmica Simons foi em busca de um novo desafio.

Quando fundou a Renaissance Technologies em 1978, sua estratégia foi usar machine learning para encontrar padrões no mercado de ações. Padrões oferecem oportunidades para ganhar dinheiro.

“A verdadeira coisa era reunir uma quantidade enorme de dados e tínhamos que obtê-los à mão nos primeiros dias. Descemos ao Federal Reserve e copiamos o histórico de juros porque não existia nos computadores.”

 Sua justificativa foi que o mercado também é complexo para qualquer um ser capaz de fazer previsões com certeza. Mas Simons havia trabalhado para os EUA Instituto de Análise de Defesa durante a Guerra Fria quebrando códigos russos extraindo padrões a partir de massas de dados.

Simons estava convencido de que uma abordagem semelhante poderia vencer o mercado.

Ele então usou seus contatos acadêmicos para contratar um grupo dos melhores cientistas que ele poderia encontrar.

Qual era então o seu critério de emprego? Se eles não sabiam nada sobre finanças, o que você estava procurando?

“Alguém com doutorado em física e que tinha cinco anos fora e tinha escrito alguns bons trabalhos e era obviamente um cara inteligente ou em astronomia ou em matemática ou em estatística. Alguém que fez ciência e fez bem.”

“Não é surpreendente que matemáticos e os físicos estão envolvidos neste campo. Em primeiro lugar, as finanças pagam muito melhor do que você imagina ser professor assistente de matemática.”

E para vários matemáticos a beleza de preços de opções é igualmente atraente para qualquer outra coisa que eles estão fazendo em suas profissões. Um deles foi Leonard Baum, um pioneiro dos modelos Markov escondidos.

Assim como Einstein percebeu que, embora não possamos observar diretamente os átomos, podemos inferir através de seu efeito sobre os grãos de pólen, os modelos ocultos de Markov visam encontrar fatores que não são diretamente observáveis, mas têm um efeito sobre o que podemos observar.

E logo depois que a Renaissance lançou seu agora famoso Fundo Medallion usando modelos de Markov ocultos e outras estratégias baseadas em dados, o Medallion Fund se tornou o fundo de investimento de maior retorno de todos os tempos.

Isso levou Bradford Cornell da UCLA em seu artigo Medallion Fund the Ultimate Counter a concluir que talvez a própria hipótese do mercado eficiente esteja errada.

Em 1988 publicou um artigo testando-o para o mercado de ações dos EUA e o que descobri foi que a hipótese é falso. Você pode realmente rejeitar a hipótese nos dados e, portanto, há previsibilidade no mercado de ações. Então é possível vencer o mercado é o que você está dizendo?

É possível vencer o mercado se você tiver os modelos certos, o treinamento certo, os recursos, o poder computacional e assim por diante. Sim.

As pessoas que encontraram os padrões no mercado de ações e a aleatoriedade para esse assunto tem sido muitas vezes físicos e matemáticos, mas seu impacto tem foi além de apenas torná-los ricos. Ao modelar a dinâmica do mercado, eles forneceram novos insights em risco e abriu novos mercados. Eles determinaram qual o preço exato dos derivativos deveriam ser e, ao fazê-lo, ajudaram a eliminar as ineficiências do mercado.

Ironicamente Se algum dia formos capazes de descobrir todos os padrões no mercado de ações sabendo quais eles são, permitam-nos eliminá-los e, finalmente, teremos um mercado perfeitamente eficiente onde todos os movimentos de preços são verdadeiramente aleatórios.

Obrigado.